Chapter 2: Bits And Data Types

Bits #

Binary digits (or bits) are the primitive unit of information in a computer system.

A bit is essentially the existence or non-existence of a voltage in a computer; any voltage which is measured close to zero(0) means a non-existent signal while anything bigger than one(1) means the existence of a signal.

A data type provides the context on what a string of bits represent ie. an integer, character code, or floating point number.

Representations #

Integers #

A data type that represents the number zero, positive, and negative whole numbers.

Unsigned Integers #

Represents positive integers and zero only.

For some number of bits $k$, there can be $0$ to $2^k - 1$ unsigned integers to be represented.

For example, if there are three(3) bits, then it can represent the unsigned integers $0$ to $2^3 - 1 = 7$.

Signed Integers #

There are three main ways to represent signed integers, these are namely:

Signed Magnitude #

Represents integers by reserving the left-most bit (also known as the sign bit) as an indicator of whether it is a positive or negative number.

For a given positive non-zero integer $k$, there is a total of $2^{k-1}$ to represent the magnitude of numbers in this representation.

For example if $k = 3$, then there are $2^{3-1} = 2^2 = 4$ total numbers to represent the positive or negative integers.

1's Complement #

Represents integers by complementing the bits: inverting the $0$ to a $1$ and vice versa.

This representation also uses a sign bit to indicate whether it is positive or negative.

For example, to get the 1's complement of the decimal number $3$, we first get its bit representation which is $3 = 011$, then complement the bits which would result in $100 = -3$.

2's Complement #

Represents integers the same way as the 1's Complement (ie. inverting the values), but has an extra step of adding a $1$ to the result.

In this representation, the sign bit represents $-2^{k-1}$.

For example to represent the decimal number $-2$ we first get its 1's Complement which is $101$, then add $1$ which results in $110$:

$110 = -2^2 + 2^1 + 0^0 = -4 + 2 = -2$

Bit Integer Arithmetic #

Addition #

Given 4-bits, adding $5 + 4$ as unsigned integers results in:

$0101 + 0100 = 1001 = 9$

Subtraction #

Given 4-bits, adding $6 - 3$ as signed integers results in:

$0110 - 1101 = 0011 = 3$

Bit Shifting #

A property of binary arithmetic is that adding a number by itself shifts the bits to the left ie. $3 + 3 = 0011 + 0011 = 0110 = 6$, this is simply because the value is multipled by [a multiple of] $2$:

$3 + 3 = 2(3)$

$= 2[0(2^3) + 0(2^2) + 1(2^1) + 1(2^0) + 0(2^{-1})]$

$= 0(2^4) + 0(2^3) + 1(2^2) + 1(2^1) + 0(2^0)$

$= 00110$

$= 0110$

$= 6$

Corollary, dividing the bits by [a multiple of] $2$ shifts it to the right:

$6 = 0110$

$6 / 2 = 2^{-1}[0(2^3) + 2(2^2) + 2(2^1) + 0(2^0) + 0(2^-1)]$

$= 0(2^2) + 2(2^1) + 2(2^0) + 0(2^{-1}) + 0(2^{-2})$

$= 0011$

$= 3$

Sign Extension #

Two bit strings with differing lengths can be processed by extending the sign bit of the smaller length bit string.

For example, given the number $21$ as a 5-bit integer and the number $-3$ as a 3-bit integer:

1. Represent $21$ in binary: $21 = 01111$
2. Represent $-3$ in binary: $-3 = 101$
3. Extend the sign-bit of $-3$ to 5-bits: $11101$
4. Now add: $01111 - 11101 = 01100 = 12$

Overflow/Underflow #

Since computers work with a finite length of bits, there comes a situation where processing bits would result in an error such as an overflow or underflow of values.

An overflow result would be when, for example, adding two signed integers goes over the maximum magnitude.

For example on a 5-bit string which has a maximum positive integer of $2^4 - 1 = 15$, adding two positive integers would result in a negative integer, for example $15 + 1 = -16$.

An underflow is the same but results in a positive integer if two negatives are processed and go over the minimum negative integer.

Bit Logical Operations #

NOT (Complement) #

Returns $0$ if the given value is $1$ and vice versa.

AND #

For two given bits $A$ and $B$, the $AND$ operator returns a $1$ iff. both $A$ and $B$ are $1$, $0$ otherwise.

AND is commonly used for bit-masking: the retrieval or extraction of specific information in a bit string.

For example, it can be used to determine if a 2's complement bit string is odd:

3 & 1 = 1; // Odd  => 011 & 001 = 001 = 1
2 & 1 = 0; // Even => 010 & 001 = 000 = 0

OR #

For two given bits $A$ and $B$, the $OR$ operator returns a $1$ iff. either $A$ or $B$ are $1$, $0$ if both $A$ and $B$ are $0$ otherwise.

XOR (Exclusive OR) #

For two given bits $A$ and $B$, the $OR$ operator returns a $1$ iff. either $A$ or $B$ are $1$ but not both.

XOR can be used to check if two bit strings are the same.

De Morgan's Law #

States two properties of composed logical operators:

1. The complement of $NOT(A)\ AND\ NOT(B)$ is equivalent to $A\ OR\ B$.

$NOT(NOT(A)\ AND\ NOT(B)) = A\ OR\ B$

2. The complement of $NOT(A)\ OR\ NOT(B)$ is equivalent to $A\ AND\ B$.

$NOT(NOT(B)\ OR\ NOT(A)) = A\ AND\ B$

Floating Point #

Is a form of scientific notation that represents Real numbers in a finite set of bits.

The most widely adopted standard to represent floating point arithmetic is the IEEE-754 standard where in a 32-bit system:

• The left-most bit is the sign bit.
• The next 8 bits are the exponent which is calculated by subtracting the excess.
• And the remaining 23 bits are the mantissa.

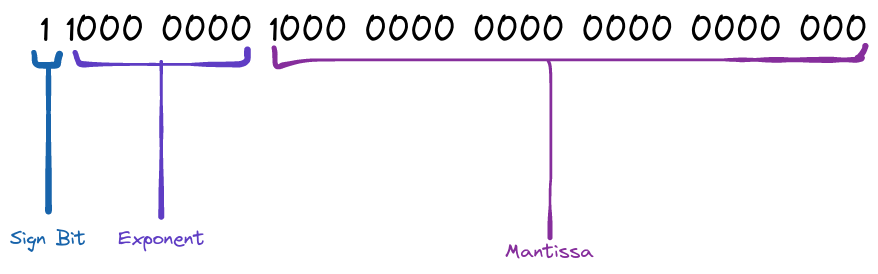
Notation:

$S \times 1.M \times 2^E$

Where:

• S is the sign bit.
• M is the mantissa.
• E is the exponent derived from some bit string that is subtracted to $127$ (the excess number). For example, if the exponent is $4$, then the bit string to represent this in floating point notation is $127 + 4 = 131 = 1000\ 0011$.

To convert a Real number to a floating point:

1. Convert the significands on the left and right sides of the radix (decimal point):
   • The left-side is derived by continuously dividing the value by 2 and retrieving the remainders.
   • The right-side is derived by continuously multiplying the value by 2 and retrieving the value on the right hand side of the result. This should have repeating patterns.
2. Move the decimal point either left or right to get the exponent.

See video for example.

ASCII #

Represents a character with a unique integer in a single byte.